Двоичное дерево поиска на JavaScript
Оригинальная статья: Christina – Understanding Binary Search Trees
В этой статье я хочу подробно рассмотреть древовидную структуру данных. Деревья представляют собой непоследовательную структуру данных, которая полезна для хранения информации, и быстрого поиска. Другими словами, они являются абстрактной моделью иерархической структуры (представьте себе семейное древо). Деревья состоят из узлов (Node) с родительско-дочерними отношениями.

Двоичное дерево и Двоичное дерево поиска
Узел в двоичном дереве или как его еще называют бинарном имеет не более двух дочерних элементов: левого и правого элемента. Это определение позволяет вам писать алгоритмы для более эффективной вставки, поиска и удаления узлов. Обратите внимание на изображение выше, чтобы увидеть двоичное дерево и ключевой словарь, который я буду использовать в этой статье.

Как вы, вероятно, можете догадаться, двоичное дерево поиска (binary search tree – BST) – это тоже двоичное дерево. Основное отличие состоит в том, что BST позволяет хранить отсортированные узлы с меньшим значением слева и узлы с большим значением справа. Как показано на рисунке выше.
Создание узлов и BST классов
Я обычно настоятельно рекомендую писать код по мере чтения статьи в каком нибудь онлайн редакторе (например https://codesandbox.io/) и постоянно тестировать / играть с тем, что мы пишем. Для начала мы создадим наш класс Node, который будет представлять узлы в нашем BST:
class Node {
constructor(data) {
this.data = data; // node value
this.left = null; // left node child reference
this.right = null; // right node child reference
}
}
Далее мы объявим базовую структуру нашего класса BinarySearchTree:
class BinarySearchTree {
constructor() {
this.root = null; // корень bst
}
}
Нашим следующим шагом будет реализация основных методов. Вот что мы рассмотрим:
insert(data)inOrderTraverse()preOrderTraverse()postOrderTraverse()search(data)remove(data)
Вставка узлов в BST
Чтобы вставить новый узел в дерево, нужно выполнить два шага:
- Проверить, является ли вставка особым случаем. Другими словами, нам нужно проверить, является ли узел, который мы пытаемся добавить, первым в дереве (то есть если какое либо значение у атрибута root). Если это так (то есть root == null), нам просто нужно указать первый (корневой) узел для этого нового узла, создав экземпляр класса Node и присвоив его корневому свойству root.
- Если первое условие не выполняется тогда просто добавить узел в соответствующую позицию.
insert(data) {
let newNode = new Node(data);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode); // helper method below
}
}
insertNode(node, newNode) {
if (newNode.data < node.data) {
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
В итоге, insert(data) создает новый узел Node со значением data и, если дерево пустое, устанавливает этот узел в качестве корня дерева, в противном случае вызывается insertNode(this.root, newNode). insertNode (node, newNode) – наш вспомогательный метод, который отвечает за сравнение данных нового узла с данными текущего узла и рекурсивное перемещение влево или вправо, соответственно, до тех пор, пока не найдет правильный узел с нулевым значением, в который можно добавить новый узел.
Проверим как это работает, и выполним следующий код …
const BST = new BinarySearchTree(); BST.insert(11); // establishes root node BST.insert(7); BST.insert(9); BST.insert(15); BST.insert(6); console.log(BST);
… мы можем проиллюстрировать последнюю вставку этой диаграммой:

Обход BST
Обход дерева (Traverse) – это процесс посещения всех узлов дерева и выполнения операции на каждом узле. Большой вопрос, как мы должны обходить дерево? Существует три общих подхода: прямой (in-order), симметричный или поперечный (pre-order) и в обратном порядке (post-order).
Прямой обход
При прямом обходе будут посещаться все узлы в порядке возрастания, начиная с указанного узла (хотя это и необязательно), и выполнять заданную функцию обратного вызова callback (также необязательно). Опять же, мы будем использовать рекурсию:
inOrderTraverse(node, callback) {
if (node != null) {
this.inOrderTraverse(node.left, callback);
callback(node.data);
this.inOrderTraverse(node.right, callback);
}
}
Следующая диаграмма показывает путь, по которому идет наш inOrderTraverse:
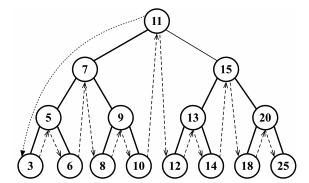
Симметричный обход
При симметричном обходе посещаются каждый узел до его потомков. Обратите внимание на довольно тонкую разницу с прямым обходом в коде и на диаграмме:
preOrderTraverse(node, callback) {
if (node != null) {
callback(node.data);
this.preOrderTraverse(node.left, callback);
this.preOrderTraverse(node.right, callback);
}
}

Обход в обратном порядке
Если вы еще не догадались, при обходе в обратном порядке посещаются узлы после посещения его потомков. Вероятно, вы можете догадаться, как будет отличаться код, но не забудьте проверить себя с помощью следующей диаграммы:
postOrderTraverse(node, callback) {
if (node != null) {
this.postOrderTraverse(node.left, callback);
this.postOrderTraverse(node.right, callback);
callback(node.data);
}
}

Поиск значений в BST
Рассмотрим вариант поиска значений в BST. В нашей реализации, node представляет текущий узел, а data представляют значение, которое мы ищем:
search(node, data) {
if (node === null) {
return null;
} else if (data < node.data) {
return this.search(node.left, data);
} else if (data > node.data) {
return this.search(node.right, data);
} else {
return node;
}
}
Я рекомендую на данном этапе протестировать весь код, вы можете добавить в console.log, чтобы можно было бы увидеть, какие узлы посещаются. Если вы не пишете код, проследите по одной из диаграмм в этой статье и спрогнозируйте путь метода search при поиске определенного значения. Вы заметите, как легко найти максимальные и минимальные значения!
Использовать метод search можно так:
...
search(node, data) {
....
else {
console.log(node)
return node;
}
...
}
...
BST.search(BST.root, 9);
Удаление узла из BST
Метод удаления является наиболее сложным методом, который мы рассмотрим в этой статье. Его сложность обусловлена различными сценариями, которые нам нужны, и еще так же потому что он рекурсивный.
// находит минимальный узел в дереве
minNode(node) {
// если слева от узла ноль тогда это должен быть минимальный узел
if (node.left === null)
return node;
else
return this.findMinNode(node.left);
}
remove(data) {
this.root = this.removeNode(this.root, data); // helper method below
}
removeNode(node, data) {
if (node === null) {
return null;
// если данные, которые нужно удалить, меньше, чем данные корня, переходим к левому поддереву
} else if (data < node.data) {
node.left = this.removeNode(node.left, data);
return node;
// если данные, которые нужно удалить, больше, чем данные корня, переходим к правому поддереву
} else if (data > node.data) {
node.right = this.removeNode(node.right, data);
return node;
// если данные такие как данные корня, удаляем узел
} else {
// удаляем узел без потомков (листовой узел (leaf) или крайний)
if (node.left === null && node.right === null) {
node = null;
return node;
}
// удаляем узел с одним потомком
if (node.left === null) {
node = node.right;
return node;
} else if(node.right === null) {
node = node.left;
return node;
}
// удаляем узел с двумя потомками
// minNode правого поддерева хранится в новом узле
let newNode = this.minNode(node.right);
node.data = newNode.data;
node.right = this.removeNode(node.right, newNode.data);
return node;
}
}
В начале мы ищем соответствующий узел, который нужно удалить, а потом есть три сценария, которые мы рассмотрим более подробно ниже.
Удаление крайнего узла (leaf node)
Первый сценарий включает в себя крайний узел (leaf node), то есть у которого нет левого или правого дочернего элемента. В этом случае нам нужно будет удалить узел, присвоив ему значение null. Однако не забывайте, что мы также должны позаботиться о ссылках из родительского узла:

Удаление узла с одним потомком
Второй сценарий включает в себя узел, который имеет левый или правый дочерний узел. Как вы можете видеть на диаграмме ниже, нам нужно пропустить соответствующий узел и назначить родительский указатель на дочерний узел:

Удаление узла с двумя потомками
Третий и последний сценарий включает в себя узел с двумя дочерними элементами. Чтобы удалить такой узел, нужно выполнить следующие действия:
- Как только вы найдете узел, который нужно удалить, найдите минимальный узел из его правого края поддерева (см. заштрихованную область на диаграмме ниже).
- Далее вы можете обновить значение узла ключом минимального узла из его правого поддерева. Этим действием вы заменяете ключ узла, что означает, что он будет удален.
- Теперь у вас есть два узла в дереве с одним и тем же ключом, что не правильно. Таким образом, нужно удалить минимальный узел из правого поддерева, поскольку вы переместили его на место удаленного узла.
- Наконец, нужно вернуть обновленную ссылку на узел его родителю.

Заключение
В этой статье мы рассмотрели алгоритмы добавления, поиска и удаления узлов из двоичного дерева поиска, а также обход дерева.
В качестве дополнения я наткнулся на этот интересный инструмент, где вы можете поиграть с интерактивным BST вместе со многими другими структурами данных, созданными Дэвидом Галлесом.
огромное спасибо! хорошее объяснение
а где описание функции findMinNode?
Вероятно опечатка) Замени в коде findMinNode на minNode. Тогда он будет вызываться рекурсивно и идти по левым веткам дерева, пока не найдет минимальный элемент (последний самый левый лист)
тут не правильный ремув