Оригинальная статья: Arpit Bhayani – Building Finite State Machines with Python Coroutines

Конечный автомат (Finite State Machine) – это математическая модель вычислений, которая моделирует последовательную логику. FSM состоит из конечного числа состояний, функций перехода, входных алфавитов, начального и конечного состояний. В области компьютерных наук автоматы используются при проектировании компиляторов, лингвистической обработки, пошаговых рабочих процессов, игрового дизайна, процедур протоколов (например, TCP / IP), программирования на основе событий, разговорного искусственного интеллекта и многих других.

Чтобы понять, что такое конечный автомат, мы можем взглянуть на дорожный светофор. Конечный автомат для него представлен ниже. Зеленый (Green) – это начальное состояние, который при получении сигнала переходит в желтый (Yellow), который, в свою очередь, при получении сигнала переходит в красный (Red). Красный затем возвращается к зеленому, и цикл продолжается.

FSM должен находиться точно в одном из конечных состояний в любой данный момент времени, а затем, в ответ на вход, который он получает, машина переходит в другое состояние. В приведенном выше примере сигнал светофора находится точно в одном из трех состояний – зеленом, желтом или красном. Правила перехода определены для каждого состояния, которые определяют, какая последовательная логика будет воспроизводиться при получение сигнала.

Реализация FSM имеет решающее значение для решения некоторых наиболее интересных проблем в области компьютерных наук, и в этой статье мы углубимся в моделирование конечного автомата с использованием корутин Python.

Корутины в Python

Прежде чем углубиться в реализацию, сделаем начальный обзор и посмотрим, что такое генераторы и корутины, как они помогут сделать реализацию FSM интуитивно понятной.

Генераторы

Генераторы – это возобновляемые функции, которые выдают значения до тех пор, пока кто-то, вызывая функцию next, продолжает спрашивать об этом. Если больше нет значений для выдачи, генератор вызывает исключение StopIteration.

def fib():
    a, b = 0, 1
    while True:
        yield a
        a, b = b, a+b

Оператор yield – это то, где происходит вся магия. По достижении оператора yield выполнение функции генератора приостанавливается, и полученное значение возвращается вызывающей стороне, и вызывающая сторона продолжает свое выполнение. Поток возвращается к генератору, когда вызывающая функция запрашивает следующее значение. Как только следующее значение запрашивается путем вызова next (явным или неявным образом), функция генератор возобновляет работу с того места, на котором она остановилась, т.е. с оператора yield.

>>> fgen = fib()
>>> [next(fgen) for _ in range(10)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

Использование генератор для генерации ряда Фибоначчи еще эффективно с точки зрения потребление памяти, так как теперь нам не нужно вычислять много чисел Фибоначчи и хранить их в памяти, в виде списка, а запрашивающий процесс может запрашивать столько значений, сколько ему нужно, и генератор будет продолжать возвращать значения по одному.

Корутины

Корутины, как и генераторы, являются возобновляемыми функциями, но вместо генерации значений они принимают значения на лету. Работа с ним очень похожа на генератор, и опять-таки, в операторе yield происходит все волшебство. Когда корутина приостанавливается в операторе yield, мы можем отправить ее значение с помощью функции send, а значение можно использовать с помощью оператора присваивания = yield, как показано ниже.

def grep(substr):
    while True:
        line = yield
        if substr in line:
            print(f"found {substr}")

В приведенном выше примере мы написали простую утилиту grep, которая проверяет подстроку в заданном потоке текста. Когда grep ставится на паузу в операторе yield, используя функцию send, мы отправляем ей текст, и после этого на него будет ссылаться переменная line. Затем корутина продолжает выполнение, чтобы проверить, находится ли substr в line или нет. Как только поток снова достигает оператора yield, корутина останавливается и ждет, пока вызывающая сторона отправит ей новое значение.

Обратите внимание, что это не поток, который продолжает работать и постоянно загружает процессор. Это просто функция, выполнение которой приостановлено в операторе yield, ее состояние сохраняется, а управление передается вызывающей стороне. После возобновления корутина начинается с того же состояния, в котором она остановилась.

Перед отправкой значения в корутину нам нужно «заправить» ее так, чтобы поток достиг оператора yield и выполнение было приостановлено в ожидании нового значения.

>>> g = grep("users/created")
>>> next(g)  # заправка генератора
>>>
>>> g.send("users/get api took 1 ms.")
>>> g.send("users/created api took 3 ms.")
found users/created
>>> g.send("users/get api took 1 ms.")
>>> g.send("users/created api took 4 ms.")
found users/created
>>> g.send("users/get api took 1 ms.")

В приведенных выше вызовах функций мы видим, как мы можем продолжать посылать текст в корутину, и она продолжает возвращать, если обнаружить заданную подстроку users/created в тексте. Эта способность корутин приостанавливать выполнение и принимать ввод на лету поможет нам смоделировать FSM очень интуитивно понятным способом.

Построение конечного автомата

При создании FSM самое важное – как мы решаем моделировать и реализовывать состояния и функции перехода. Состояния могут быть смоделированы как корутины Python, которые выполняют бесконечный цикл, в рамках которого они принимают ввод, решают переход и обновляют текущее состояние FSM. Функция перехода может быть такой же простой, как набор операторов if и elif, а в более сложной системе это может быть функция принятия решения.

Чтобы погрузиться в детали низкого уровня, мы строим FSM для регулярного выражения ab*c, что означает, что если данная строка соответствует регулярному выражению, то машина должна завершиться в конечном состоянии, только тогда мы говорим, что строка соответствует регулярному выражению.

Состояние

Исходя из вышесказанного, смоделируем состояние q2 как

def _create_q2():
    while True:
        # Подождем, пока ввод не будет получен.
        # после получения сохраним ввод в `char`
        char = yield

        # в зависимости от того, что мы получили
        # в качестве входных данных
        # изменить текущее состояние fsm
        if char == 'b':
            # при получении `b` состояние перемещается в` q2`
            current_state = q2
        elif char == 'c':
            # при получении `c` состояние перемещается в` q3`
            current_state = q3
        else:
            # при получении любого другого ввода, разорвать петлю
            # чтобы в следующий раз, когда кто-нибудь отправит
            # корутину вызываем StopIteration
            break

корутина работает как бесконечный цикл, в котором она ожидает входной токен в операторе yield. Получив вход, скажем, b, она меняет текущее состояние FSM на q2, а при получении c меняет состояние на q3, и это именно то, что мы видим на диаграмме FSM.

Класс FSM

Для сохранения инкапсуляции мы определим класс для FSM, который содержит все состояния и поддерживает текущее состояние машины. Он также будет иметь метод send, который перенаправляет полученный ввод в current_state. При получении ввода с помощью current_state мы сможем принять решение о следующем состояние и обновить current_state FSM, как показано выше.

В зависимости от варианта использования у FSM также может быть функция, которая отвечает на основные проблемы, например, соответствует ли данная строка регулярному выражению? или делится число на 3?

Класс FSM для регулярного выражения ab*c может быть смоделирован следующим образом:

class FSM:
    def __init__(self):
        # инициализация
        self.start = self._create_start()
        self.q1 = self._create_q1()
        self.q2 = self._create_q2()
        self.q3 = self._create_q3()
        
        # установка текущего состояния системы
        self.current_state = self.start

        # флаг остановки, чтобы обозначить,
        # что итерация остановлена из-за плохого
        # входа, для которого переход не был определен.
        self.stopped = False

    def send(self, char):
        """Функция отправляет текущий ввод в current_state. Она захватывает исключение StopIteration и помечает флаг stopped.
        """
        try:
            self.current_state.send(char)
        except StopIteration:
            self.stopped = True
        
    def does_match(self):
        """Функция в любой момент времени возвращает True если
 текущее состояние соответствует заданному регулярному выражению.  Это делается путем сравнения текущего состояния с конечным состоянием `q3`.
         Она также проверяет наличие флага stopped, который назначается, при неправильного вводе и дальнейшея итерация FSM должна была быть остановлена.
        """
        if self.stopped:
            return False
        return self.current_state == self.q3

    ...
    
    @prime
    def _create_q2(self):
        while True:
            # Ждем, пока ввод не будет получен.
            # после получения сохраняем ввод в `char`
            char = yield

            # в зависимости от того, что мы получили в 
            # качестве входных данных
            # изменяем текущее состояние fsm
            if char == 'b':
                # при получении `b` состояние перемещается в` q2`
                self.current_state = self.q2
            elif char == 'c':
                # при получении `c` состояние перемещается в` q3`
                self.current_state = self.q3
            else:
                # при получении любого другого ввода, останавливаем цикл
                #  чтобы в следующий раз, когда кто-нибудь что-нибудь
                # отправит вызывать StopIteration
                break
    ...

Подобно тому, как мы определили функцию _create_q2, мы определяем функции для других трех состояний start, q1 и q3. Вы можете найти полный смоделированный FSM, в arpitbbhayani/fsm/regex-1

Функция Driver

Мотивом этой постановки задачи является определение функции с именем grep_regex, которая проверяет данный текст на соответствие регулярному выражению ab*c. Функция создаст экземпляр FSM и передаст ему поток символов. После того, как все символы будут получены, вызывается функция does_match, которая определить, соответствует ли данный text регулярному выражению ab*c или нет.

def grep_regex(text):
    evaluator = FSM()
    for ch in text:
        evaluator.send(ch)
    return evaluator.does_match()

>>> grep_regex("abc")
True

>>> grep_regex("aba")
False

Все выполняется чисто последовательное – и это из-за корутины. Кажется, что все состояния работают параллельно, но все они выполняются в одном потоке одновременно. Корутина current state выполняется, в то время как все остальные будут приостановлены в своих соответствующих операторах yield. Когда новый входной сигнал отправиться в коррутину, она разблокируется, завершит свое выполнение, изменит current_state FSM и снова приостанавит свое выполнение в операторе yield.

Больше FSMs

Мы увидели, насколько интуитивно понятно создавать автоматы регулярного выражения с использованием Python корутин, но если наша гипотеза верна, то все должно быть одинаково интуитивно понятно, когда мы реализуем автоматы для других случаев использования, и здесь мы рассмотрим два примера и посмотрим, как это состояние. реализовано в каждом

Делимость на 3

Здесь мы строим FSM, который сообщает, делится ли данный поток цифр чисел на 3 или нет. Конечный автомат, показано ниже.

Мы можем реализовать состояние q1 через корутину

def _create_q1(self):
    while True:
        digit = yield
        if  digit in [0, 3, 6, 9]:
            self.current_state = self.q1
        elif  digit in [1, 4, 7]:
            self.current_state = self.q2
        elif  digit in [2, 5, 8]:
            self.current_state = self.q0

Мы можем увидеть сходство между реализацией корутин и функцией перехода состояний. Полная реализация этого FSM находится в arpitbbhayani/fsm/divisibility-by-3.

SQL Query Валидатор

Здесь мы создаем FSM для SQL Query Validator, который для полученного SQL-запроса сообщает, является ли он допустимым SQL-запросом или нет. FSM для валидатора, который охватывает все запросы SQL, будет массивным, поэтому мы просто взяли его подмножество, где мы поддерживаем следующие запросы SQL

SELECT * from TABLE_NAME;
SELECT column, [...columns] from TABLE_NAME;

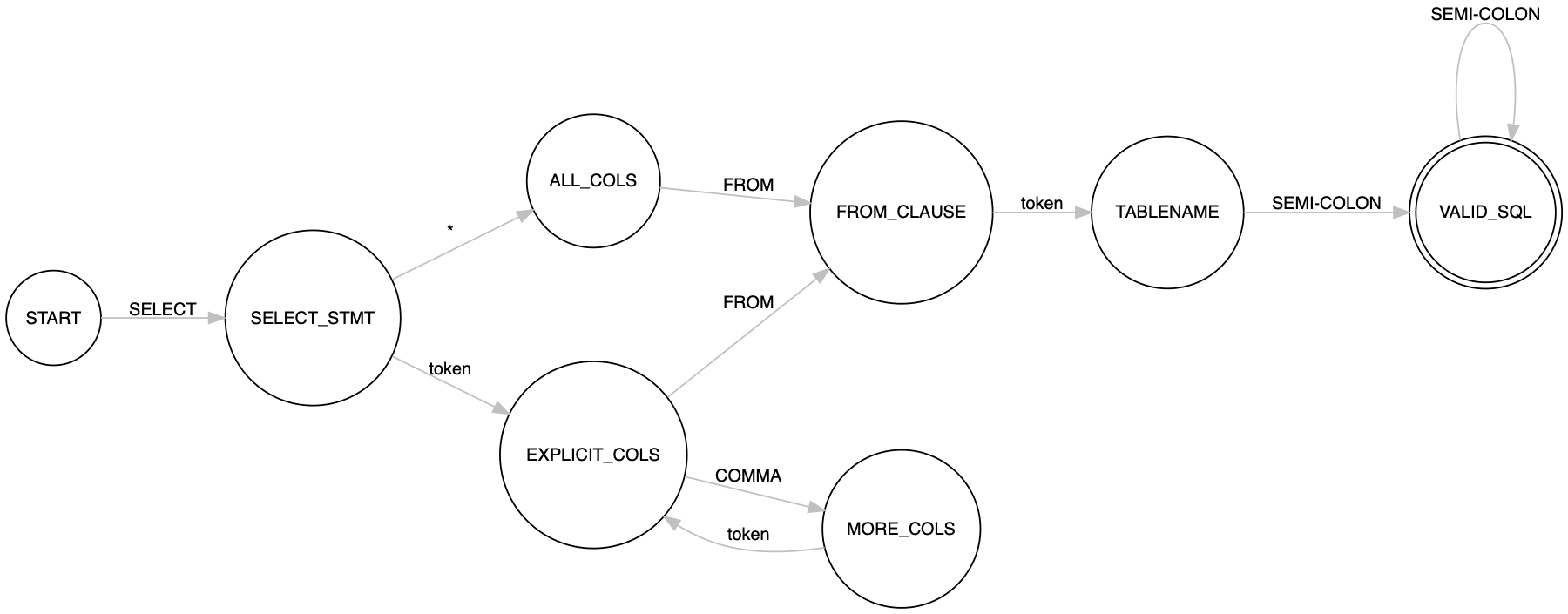
Мы можем реализовать состояние explicit_cols как корутину,

def _create_explicit_cols(self):
    while True:
        token = yield
        if token == 'from':
            self.current_state = self.from_clause
        elif token == ',':
            self.current_state = self.more_cols
        else:
            break

Опять же, корутина, посредством которой реализуется состояние, очень похожа на функцию перехода состояния, сохраняющую свою простоту. Всю реализацию этого FSM можно найти в arpitbbhayani/fsm/sql-query-validator.

Заключение

Хотя это может быть не самый эффективный способ реализации и построения FSM, но на самом деле это самый интуитивный способ. Ребра и переходы состояний хорошо транслируются в операторы if и elif или функции принятия решений, в то время как каждое состояние моделируется как независимая корутина, и мы все еще делаем вещи последовательным образом. Все исполнение похоже на эстафету, где эстафету исполнения передают от одной корутины к другой.

Рекомендации и чтения

• Finite State Machines – Wikipedia
• Finite State Machines – Brilliant.org
• FSM Applications
• What Are Python Coroutines?
• How to Use Generators and yield in Python