Эта отрывок из бесплатной книги “Парадигмы алгоритмического проектирования (жадные алгоритмы, разделяй и властвуй и динамическое программирование)” –Brandon Algorithmic Design Paradigms (Greedy, Divide & Conquer, and Dynamic Programming).. ✨

Вариант в PDF (оригинал)

Книга также есть на GitHub. 😁brandonskerritt/AlgorithmsBook GitHub

Жадные алгоритмы

Жадные алгоритмы это такие алгоритмы, которые стремятся сделать оптимальный выбор в каждый момент времени. На каждом шагу выбирается лучший выбор, не задумываясь о будущем.

Почему жадные алгоритмы называются жадными?

Алгоритмы называются жадными, когда они используют жадное свойство. Жадное свойство:

В каждый момент времени, что есть лучший выбор?

Жадные алгоритмы – жадные. Они не смотрят в будущее, чтобы выбрать глобальное оптимальное решение. Их интересует только лучшее решение в данный момент. Но общее оптимальное решение может отличаться от решения, которое выбирает алгоритм на каждом шаге своей работы. Так же они никогда не оглядываются назад на то, что сделали, чтобы понять, нужна ли глобальная оптимизация. В этом главное отличие жадного и динамического программирования.

---

Для чего используются жадные алгоритмы?

Жадные алгоритмы очень быстрые. Намного быстрее, чем две другие альтернативы (Разделяй и властвуй – Divide & Conquer, и Динамическое программирование Dynamic Programming). Они популярные, потому что они быстрые.

Примеры популярных жадных алгоритмов:

• Dijkstra’s Algorithm (Алгоритм Дейкстры)
• Kruskal’s algorithm (Алгоритм Крускала)
• Prim’s algorithm (Алгоритм Прима)
• Huffman trees (Деревья Хаффмана)

Мы собираемся рассмотреть жадные алгоритмы, на известном примере – подсчет выдачи сдачи. Это не так сложно для этой парадигмы.

---

Как мне создать жадный алгоритм?

Ваш алгоритм должен всегда отвечать на этот вопрос:

Каков лучший выбор в этот момент времени?

Вот и все. Не так уж и много. Жадные алгоритмы, как правило, легче кодировать, чем «разделяй и властвуй»(Divide & Conquer) или динамическое программирование (Dynamic Programming).

---

Подсчет выдачи сдачи используя жадность

Представьте, что вы торговый автомат. Кто-то дает вам £1 и покупает напиток за £0,70. В фунте стерлингов нет монеты 30 пенсов (30p). Как рассчитать, сколько сдачи вернуть?

Для справки, номинал каждой монеты в Великобритании:

1p, 2p, 5p, 10p, 20p, 50p, £1

Жадный алгоритм начинается с самого высокого номинала и работает в обратном направлении. Наш алгоритм начинается с £1.
£1 фунт больше, чем 30 пенсов, поэтому он не может его использовать. Далее смотрим на 50р, видим то же самое. Потом 20р. 20p<30p, поэтому требуется 1 монета 20p.

Теперь алгоритм должен вернуть сдачу еще на 10p. Он снова пробует 20p, но 20p> 10p. Затем идет до 10р. Он выбирает 1 монету на 10p, и теперь возвращается 0, мы останавливаем алгоритм.

Итого мы возвращаем 1x20p и 1x10p.

Этот алгоритм работает довольно хорошо в реальной жизни. Давайте рассмотрим другой пример, на этот раз у нас есть номинал и количество этой монеты в автомате в формате (номинал, количество).

(1p, 10), (2p, 3), (5p, 1), (10p, 0), (20p, 1p), (50p, 19p), (100p, 16)

Алгоритм попросили снова вернуть сдачу на 30p. 100р (£ 1) – это нет. То же самое для 50. Далее 20p, мы можем сделать это. Мы выбираем 1x 20p. Теперь нам нужно вернуть 10р. 20p закончилось, поэтому мы идем вниз на 1 номинал.

10p закончилось, поэтому мы идем далее вниз еще на 1 номинал.

У нас 5p, поэтому мы выбираем 1x5p. Теперь нам нужно вернуть еще 5р. Проверяем 5p но они закончились, поэтому мы спускаемся вниз.

Мы выбираем 1 монету на 2p. Теперь нам нужно вернуть 3р. Мы выбираем еще 2 монеты. Теперь нам нужно вернуть 1р. Мы спускаемся еще раз вниз. Тут мы выбираем 1x1p монета.

В общем, наш алгоритм выбрал следующие монеты, чтобы вернуть сдачу:

# (значение монеты, количество монет)
(10, 1)
(5, 1)
(2, 2)
(1, 1)

Давайте теперь закодируем это. Во-первых, нам нужно определить проблему. Начнем с условий.

# типы значений монет
denominations = [1, 2, 5, 10, 20, 50, 100]
# 100p is £1

Теперь перейдем к основной функции. С учетом номиналов и суммы для внесения изменений мы хотим вернуть список того, сколько раз эта монета была возвращена.

Если наш список denominations такой же, как указано выше, то [6, 3, 0, 0, 0, 0, 0] представляет собой взятие 6 монет 1p и 3 монет 2p, но 0 всех других монет.

denominations = [1, 2, 5, 10, 20, 50, 100]
# 100p is £1

def returnChange(change, denominations):
    toGiveBack = [0] * len(denominations)
    for pos, coin in reversed(list(enumerate(denominations))):

Создаем полный список denominations и отствующие значения заполним нулями.

Мы хотим пройтись от самого большого до самого маленького. Reversed(x) переворачивает x и позволяет нам зацикливаться в обратном направлении. Enumerate означает «цикл по этому списку, но сохраняйте позицию в другой переменной». В нашем примере, когда мы запускаем цикл. coin = 100 и pos = 6.

Наш следующий шаг – многократный выбор монеты, пока мы можем использовать эту монету. Если нам нужно дать сдачу change = 40, мы хотим, чтобы наш алгоритм выбрал 20, затем снова 20, пока он больше не сможет использовать 20. Мы делаем это с помощью цикла for.

denominations = [1, 2, 5, 10, 20, 50, 100]
# 100p is £1

def returnChange(change, denominations):
    # делам список toGiveBack размером с denominations
    toGiveBack = [0] * len(denominations)

    # проходим по всему denominations
    # с сохраненим coin и pos.
    for pos, coin in enumerate(reversed(denominations)):
        # пока coin меньше или равно change
        while coin <= change:

В то время как coin все еще меньше или равно change, добавим эту coin в наш список возврата toGiveBack и удалим ее из сдачи.

denominations = [1, 2, 5, 10, 20, 50, 100]
# 100p is £1

def returnChange(change, denominations):
    toGiveBack = [0] * len(denominations)

    for pos, coin in enumerate(reversed(denominations)):
        while coin <= change:
            change = change - coin
            toGiveBack[pos] += 1
    return(toGiveBack)

print(returnChange(30, denominations))
# вернет [0, 0, 0, 1, 1, 0, 0]
# 1x 10p, 1x 20p

Сложность выполнения этого алгоритма (О большое) определяется двумя циклами, поэтому оно равно O(n²⁾.

---

Является ли жадный алгоритм лучшим? Жадность всегда работает?

То что оптимально на локальном уровне, иногда не оптимально на глобальном уровне. В алгоритме подсчете сдачи мы можем определить точку, в которой он не является лучшим в глобальном масштабе.

Допустим у нас есть условие:

• пусть у нас будет монеты трех номиналов [1p, 15p, 25p].

И нас попросим выдать сдачу в 30 пенсов. Теперь посмотрим, что вернет наш алгоритм.

[5, 0, 1]

То есть он выбирает 1x25p и 5x1p. Хотя лучшим решением будет – 2х15р.

Наш алгоритм потерпел неудачу, потому что он вообще не смотрел на 15p. Он первым делом посмотрел на 25р и подумал: «Да, это подходит. Давайте возьмем это».

Затем он посмотрел на 15p и подумал, что «это не подходит, давайте двигаться дальше» (так как 25 + 15 > 30).

Это пример того, где жадные алгоритмы не лучший выбор.

Чтобы обойти это, вам нужно будет либо создать валюту, где это не работает, либо использовать перебор решений. Или используйте динамическое программирование.

Но жадные алгоритмы иногда могут быть лучшими на глобальном уровне то есть глобально оптимальными . Ранее мы видели, что эти алгоритмы глобально оптимальны:

• Dijkstra’s Algorithm
• Kruskal’s algorithm
• Prim’s algorithm
• Huffman trees

Существуют и другие глобально оптимальные решения, но жадные алгоритмы быстрее и проще в программировании, чем другие решения.

---

Алгоритм Дейкстры

Алгоритм Дейкстры находит кратчайший путь от узла ко всем остальным узлам графа. В нашем примере мы будем использовать взвешенный ориентированный граф. У каждого ребра есть направление, и у каждого ребра есть вес.

Алгоритм Дейкстры имеет много применений. Он может быть очень полезен в дорожных сетях, где вам нужно найти самый быстрый маршрут к месту. Алгоритм также используется для:

• IP Routing
• A* Algorithm
• Telephone networks

Алгоритм следует следующим правилам:

1. Каждый раз, когда мы хотим посетить новый узел, мы выберем узел с наименьшим известным расстоянием.
2. Как только мы переместились в узел, мы проверяем каждый из соседних узлов. Мы вычисляем расстояние от соседних узлов до корневых узлов, суммируя стоимость ребер, которые ведут к этому новому узлу.
3. Если расстояние до узла меньше известного расстояния, мы обновим самое короткое расстояние.

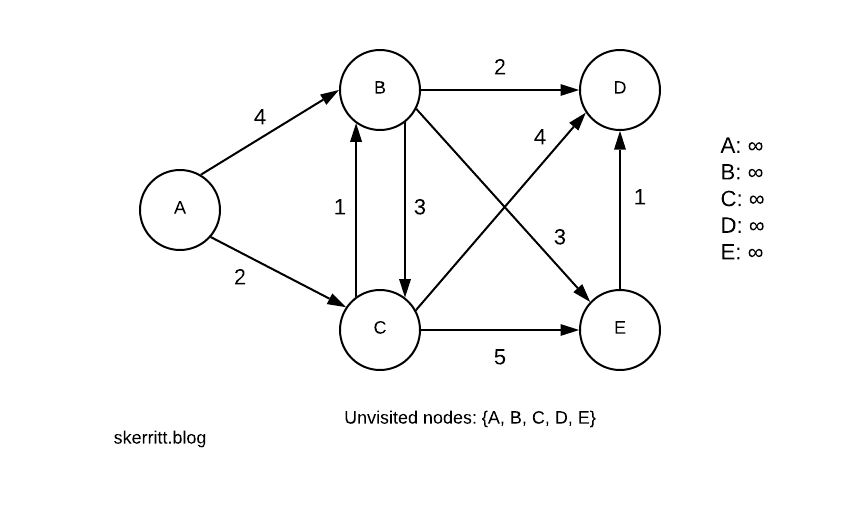
Наш первый шаг – выбрать начальный узел. Давайте выберем A. Все расстояния назначаются равными бесконечности, так как мы пока не знаем их расстояния, пока не достигнем узла, который знает расстояние.

Мы отмечаем A в нашем списке не посещенных узлов. Расстояние от A до A равно 0. Расстояние от A до B равно 4. Расстояние от A до C равно 2. Наш список расстояний с правой стороны рисунка.

Затем мы выбираем наименьшее ребро, где вершина не была выбрана. Наименьшее ребро A ->C, и мы еще не выбрали C. Далее мы посещаем С.

Обратите внимание, как мы выбираем наименьшее расстояние от нашего текущего узла до узла, который мы еще не посетили. Мы жадные. В этом случае жадный метод является глобальным оптимальным решением.

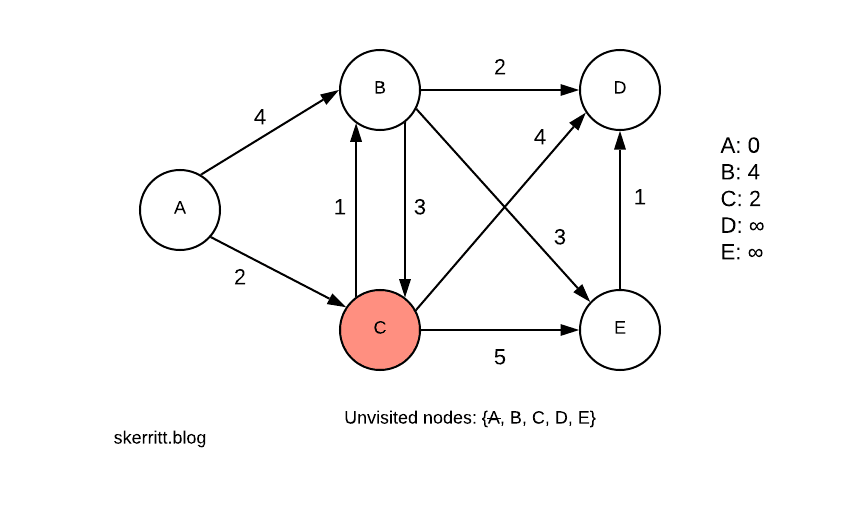
Мы можем добраться до B из C. Теперь нам нужно выбрать минимум. min(4, 2 + 1) = 3.

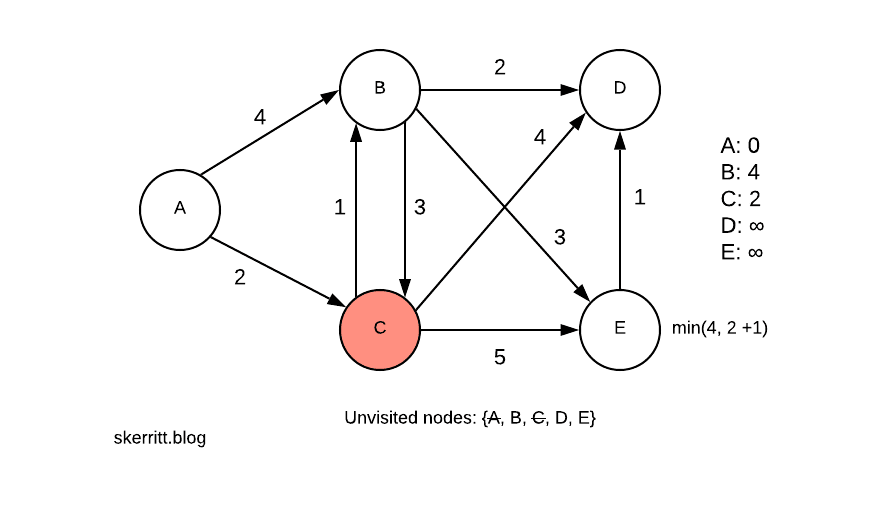
Поскольку A->C->B меньше, чем A->B, мы обновляем B этой информацией. Затем мы добавляем расстояния от других узлов, которые теперь можем достичь.

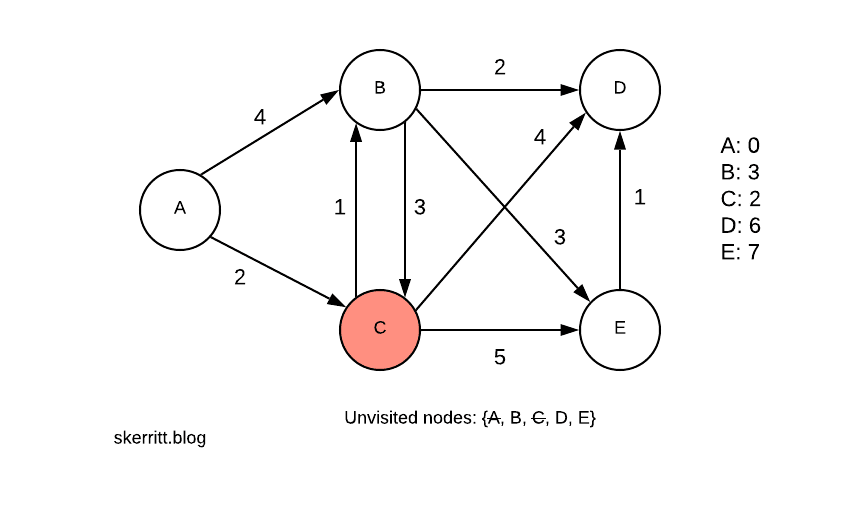
Наша следующая наименьшая вершина с узлом, который мы еще не посетили, это B, с 3. Мы посещаем B.

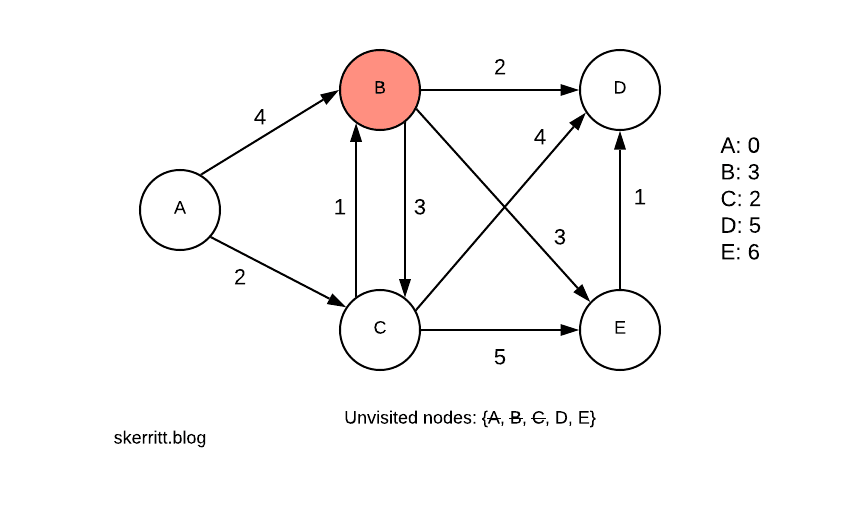
Мы делаем то же самое для B. Затем мы выбираем самую маленькую вершину, которую мы еще не посетили, D.

На этот раз мы не обновляем расстояния. Наш последний узел тогда E.

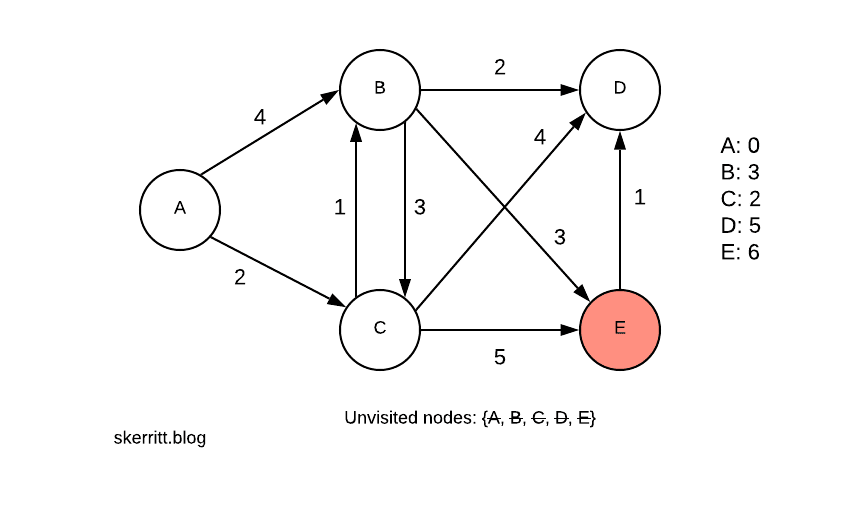
Там нет обновлений снова. Чтобы найти кратчайший путь от A до других узлов, мы пройдемся по нашему графику.

Сначала мы выбираем A, затем C, а затем B. Если вам нужно создать кратчайший путь от A до каждого другого узла в виде графика, вы можете запустить этот алгоритм, используя таблицу с правой стороны.

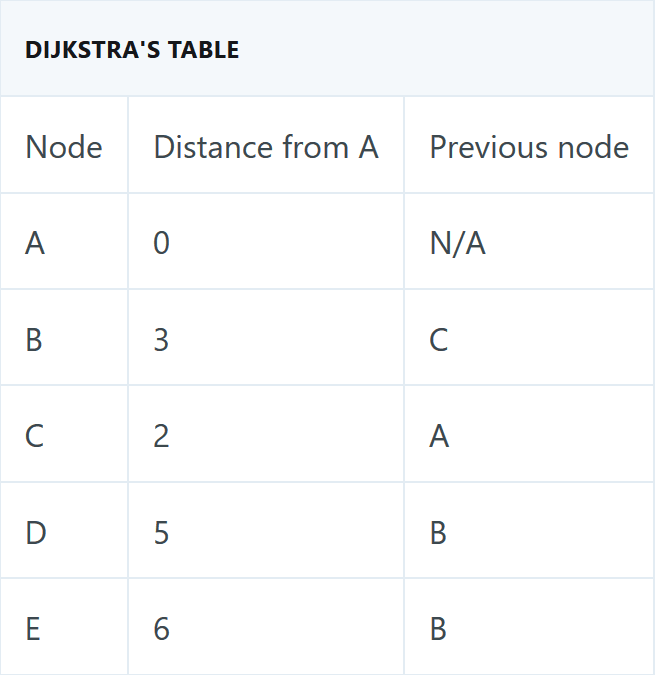
Используя эту таблицу легко нарисовать кратчайшее расстояние от A до каждого другого узла на графике:

---

Дробная задача о ранце с использованием жадного алгоритма

Представь, что ты вор. Ты врываешься в дом Джуди Холлидей – обладателя Оскара 1951 года за лучшую женскую роль. Джуди кладезь драгоценных камней. Дом Джуди выложен до краев драгоценными камнями.

Ты принес с собой сумку – рюкзак. Максимальный вместимость этой сумки – 7 пунктов веса. У тебя был список всех предметов Джуди из какой-то страховой бумаги. Пункты читаются как:

Первым шагом к решению проблемы дробного ранца является расчет стоимости/веса для каждого предмета.

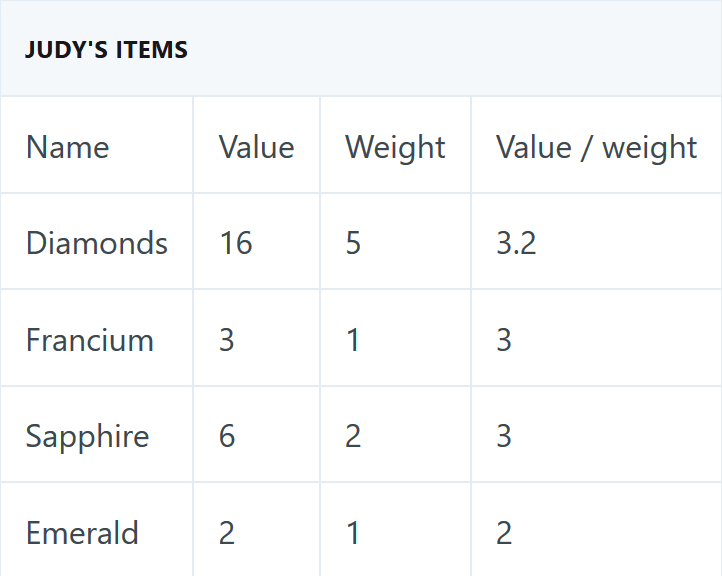
И теперь мы жадно отбираем самые крупные. Для этого мы можем отсортировать их по значению/весу в порядке убывания. К счастью для нас, они уже отсортированы. Самый большой – 3,2.

knapsack value = 16
knapsack total weight = 5 (out of 7)

Затем мы выбираем Francium (я знаю, что это не драгоценный камень, но Джуди немного странная 😉)

knapsack value = 19
knapsack weight = 6

Теперь мы добавляем Сапфир. Но если мы добавим Сапфир, наш общий вес достигнет 8 пунктов.

В задаче дробного ранца мы можем разрезать предметы, чтобы взять их дроби. У нас в сумке осталось 1 пункт веса. Наш сапфир имеет вес 2 пункта. Мы рассчитываем соотношение:

Свободное место в рюкзаке / вес товара

А затем умножьте это соотношение на стоимость предмета, чтобы узнать, сколько стоимости этого предмета мы можем взять.

1/2 * 6 = 3

knapsack value = 21
knapsack weight = 7

Жадный алгоритм может оптимально решить проблему дробного ранца, но он не может оптимально решить проблему ранцев {0, 1}. В этой задаче вместо того, чтобы брать часть элемента, вы либо берете его {1}, либо не берете {0}. Чтобы решить эту проблему, вам нужно использовать динамическое программирование.

Сложность алгоритма для него O(n log n). Расчетное значение/вес O (1). Наш основной шаг – сортировка по наибольшему значению/весу, что занимает O(n log n) времени.

---

Заключение

Жадные алгоритмы очень быстрые, но не всегда могут обеспечить глобальное лучшее решение. Но обычно они проще и легче кодируются, чем их аналоги.

Следующая часть: Алгоритмы – часть 2. Разделяй и властвуй.