Алгоритмы — часть 2. Разделяй и властвуй.

13.11.201915.11.2019 Editorial Team 0 Comments Алгоритмы16 781 просмотров

Spread the love

Продолжаем перевод бесплатной книги «Парадигмы алгоритмического проектирования (жадные алгоритмы, разделяй и властвуй и динамическое программирование)» —Brandon Algorithmic Design Paradigms (Greedy, Divide & Conquer, and Dynamic Programming).. ✨

Предыдущая глава: Алгоритмы – часть 1. Жадные алгоритмы, алгоритм Дейкстры.

Алгоритмы «разделяй и властвуй» на самом деле редко описываются в учебниках по программированию, но я считаю что их должен знать каждый программист. Алгоритмы «разделяй и властвуй» являются основой параллелизма и многопоточности.

Я часто слышу о том, как можно оптимизировать цикл for для ускорения или как операторы switch немного быстрее, чем операторы if. Но мы часто не замечаем, что большинство компьютеров имеют более одного ядра с возможностью поддержки нескольких потоков. И прежде чем беспокоиться об оптимизации циклов и т.п. что если пытаются взглянуть на проблему оптимизации под другим углом.

Разделяй и властвуй — один из способов решения проблем оптимизации под другим углом. В этой статье я расскажу о алгоритме «разделяй и властвуй» и что это такое. Не беспокойтесь, если у вас нет опыта или знаний по этой теме. Эта статья предназначена для новичков в области программирования.

Я собираюсь рассмотреть этот алгоритм на 3 примерах. Первым будет простое объяснение. Вторым будет некоторый код. И в финал войдет в математическое ядро техники «разделяй и властвуй». (Не волнуйтесь, я тоже ненавижу математику).

Что такое разделяй и властвуй? 🌎

Разделяй и властвуй — это алгоритм, в котором ты разделяешь большую проблему на множество более мелких, которых будет гораздо проще решить. Небольшой пример ниже иллюстрирует это.

A Gentle Introduction to Divide and Conquer Algorithms — Источник: https://res.cloudinary.com/practicaldev/image/fetch/s—SH7zC_ey—/c_limit%2Cf_auto%2Cfl_progressive%2Cq_auto%2Cw_880/https://skerritt.blog/content/images/2019/03/Blank-Diagram-14-.png

Мы берем уравнение «3 + 6 + 2 + 4» и разбиваем его на наименьший возможный набор уравнений, который равен [3 + 6, 2 + 4]. Это также может быть [2 + 3, 4 + 6]. Порядок не имеет значения, пока мы превращаем это одно длинное уравнение во многие меньшие уравнения.

Допустим, у нас есть 8 номеров:

И мы хотим сложить их все вместе. Сначала мы разделим задачу на 8 равных подзадач. Мы делаем это, разбивая сложение на отдельные части.

Затем мы начинаем складывать по 2 номера одновременно.

Затем 4 числа в 8 чисел, что является нашим результатом.

Почему мы разбиваем его на отдельные номера на этапе 1? Почему бы нам просто не начать со стадии 2? Потому что, хотя этот список чисел четен, если бы он был нечетным, вам нужно разбить его на отдельные числа, чтобы лучше с ним справиться.

Алгоритм «разделяй и властвуй» пытается разбить проблему на как можно большее количество маленьких кусков, поскольку ее легче решить с помощью маленьких кусочков. Обычно это делается с помощью рекурсии.

Формально техника, определена в известной книге «Introduction to Algorithms» Кормена, Лизерсона, Ривеста и Штейна:

1. Разделяй

Если проблема небольшая, то решайте ее напрямую. В противном случае разделите задачу на меньшие подмножества той же проблемы.

2. Властвуй

Решайте меньшие проблемы, решая их рекурсивно. Если подзадачи достаточно малы, рекурсия не нужна, и вы можете решить их напрямую.

Рекурсия — это когда функция вызывает себя. Возможно это трудно понять, если вы никогда не слышали об этом раньше. Вот пример помогающий это понять:

n = 6

def recur_factorial(n):
   if n == 1:
       return n
   else:
       return n * recur_factorial(n-1)

print(recur_factorial(n))

Я полностью объясню это код через секунду.

3. Комбинируй

Возьмите решения для подзадач и объедините это с решением исходной проблемы.

Рассмотрим пример выше. Разделительная часть является частью рекурсии. Мы делим задачу в строке return n * recur_factorial(n-1).

Точнее, в recur_factorial (n-1) мы разделяем проблему.

Часть «властвуй» — это тоже часть рекурсии, но также и оператор if. Когда проблема достаточно мала, мы решаем ее напрямую (return n). Иначе, мы выполняем return n * recur_factorial (n-1).

Комбинирование. Мы делаем это с помощью символа умножения. В конце концов, мы возвращаем факториал числа. Если бы у нас там не было символа, и код возвращал return recur_factorial(n-1), то бы не было комбинирования и мы бы ничего не получили бы , отдаленно похожего на факториал. (В этом случае мы бы получили бы 1, для тех, кому интересно).

Продолжим далее изучение, то как работает принцип «разделяй и властвуй» на некоторых известных алгоритмах, сортировке слиянием и алгоритме Ханойских башен.

Сортировка слиянием 🤖

Merge Sort — это алгоритм сортировки. Алгоритм работает следующим образом:

Разделяем последовательность из n чисел на 2 половины
Рекурсивно сортируем две половинки
Объединяем две отсортированные половины в одну отсортированную последовательность

На этом изображении мы разбиваем 8 чисел на отдельные цифры. Так же, как мы делали ранее. Как только мы это сделаем, мы можем начать процесс сортировки.

Сравнивает 51 и 13. Поскольку 13 меньше, то помещаем ее в левую часть. Так же делаем для (10, 64), (34, 5), (32, 21).

Потом объединяем (13, 51) с (10, 64). Мы знаем, что 13 является самым маленьким в первом списке, а 10 — самым маленьким в правом списке. 10 меньше 13, поэтому нам не нужно сравнивать 13 с 64. Мы сравниваем и объединяем два отсортированных списка.

В рекурсии мы используем термин базовый случай (base case) для обозначения наименьшего абсолютного значения, с которым мы можем иметь дело. При сортировке слиянием базовый случай равен 1. Это означает, что мы разбиваем список до тех пор, пока не получим подсписок длиной 1. Именно поэтому мы опускаемся до 1, а не 2. Если базовый случай равен 2, мы остановился бы на номере 2.

Если длина списка (n) больше 1, то мы делим список и каждый подсписок на 2, пока не получим подсписок размером 1. Если n = 1, список уже отсортирован, поэтому мы ничего не делаем ,

Сортировка слиянием является примером алгоритма «разделяй и властвуй». Давайте рассмотрим еще один алгоритм, чтобы действительно понять, как работает принцип «разделяй и властвуй».

Забавное видео сортировки в виде танца:

Далее закодируем сортировку слиянием. Источником в этом случае будет Merge sort walkthrough with code in Python
Сслыка на Jupyter notebook здесь.

Нам понадобится всего две функции split и merge_sorted_lists

Шаг 1 — Создаем функцию разделения

Исходный список, будет делится на два списка прямо посередине

def split(input_list):
    """
    Splits a list into two pieces
    :param input_list: list
    :return: left and right lists (list, list)
    """

    input_list_len = len(input_list)
    midpoint = input_list_len // 2
    return input_list[:midpoint], input_list[midpoint:]

Список входных и ожидаемых результатов:

[
    ({'input_list': [1, 2, 3]}, ([1], [2, 3])),
    ({'input_list': [1, 2, 3, 4]}, ([1, 2], [3, 4])),
    ({'input_list': [1, 2, 3, 4, 5]}, ([1, 2], [3, 4, 5])),
    ({'input_list': [1]}, ([], [1])),
    ({'input_list': []}, ([], []))
]

Каждый элемент в списке соответствует кортежу. Первый элемент кортежа — это входные данные, а второй элемент содержит левый и правый список. Например, первый список — это [1, 2, 3], в результате получаем — [1] и [2, 3] для левого и правого списка.

Шаг 2 — Создаем функцию объединения отсортированных списков

В ней будем объединять два заранее отсортированных списка в один.

def merge_sorted_lists(list_left, list_right):
    # Особый случай: один или два списка пусты
    if len(list_left) == 0:
        return list_right
    elif len(list_right) == 0:
        return list_left
    
    index_left = index_right = 0
    list_merged = []  # list to build and return
    list_len_target = len(list_left) + len(list_right)

    while len(list_merged) < list_len_target:
        if list_left[index_left] <= list_right[index_right]:
            # Значение левого списка меньше
            list_merged.append(list_left[index_left])
            index_left += 1
        else:
            # Значение правого списка меньше
            list_merged.append(list_right[index_right])
            index_right += 1
            
        # Проверяем на конец списка
        if index_right == len(list_right):
            # Достигнут конец справа
            list_merged += list_left[index_left:]
            break
        elif index_left == len(list_left):
            # Достигнут конец слева
            list_merged += list_right[index_right:]
            break
        
    return list_merged

Примеры результата выполнения

[
    ({'list_left': [1, 5], 'list_right': [3, 4]}, [1, 3, 4, 5]),
    ({'list_left': [5], 'list_right': [1]}, [1, 5]),
    ({'list_left': [], 'list_right': []}, []),
    ({'list_left': [1, 2, 3, 5], 'list_right': [4]}, [1, 2, 3, 4, 5]),
    ({'list_left': [1, 2, 3], 'list_right': []}, [1, 2, 3]),
    ({'list_left': [1], 'list_right': [1, 2, 3]}, [1, 1, 2, 3]),
    ({'list_left': [1, 1], 'list_right': [1, 1]}, [1, 1, 1, 1]),
    ({'list_left': [1, 1], 'list_right': [1, 2]}, [1, 1, 1, 2]),
    ({'list_left': [3, 3], 'list_right': [1, 4]}, [1, 3, 3, 4]),
]

Шаг 3 — Сортировка слиянием

Сортировка слиянием будет использовать только 2 предыдущие функции
Будем делить списки, пока они в них не окажется по одному элементу
Будем сортировать только списки с одним элементом
И в конце объединим одноэлементные (или пустые) списки

def merge_sort(input_list):
    if len(input_list) <= 1:
        return input_list
    else:
        left, right = split(input_list)
        # Следующая строка является наиболее важной
        return merge_sorted_lists(merge_sort(left), merge_sort(right))

Пример результата выполнения

[
    ({'input_list': [1, 2]}, [1, 2]),
    ({'input_list': [2, 1]}, [1, 2]),
    ({'input_list': []}, []),
    ({'input_list': [1]}, [1]),
    ({'input_list': [5, 1, 1]}, [1, 1, 5]),
    ({'input_list': [9, 1, 10, 2]}, [1, 2, 9, 10]),
]

Рассмотрим как работает сортировка

merge_sort будет разбивать список до тех пор, пока он не доберется до одноэлементных списков. Как только это произойдет (базовый случай рекурсии), начинает работать merge_sorted_list. Для следующего примера вот что происходит:

input_list=[9, 1, 10, 2]
left=[9, 1] и right=[10, 2]
merge_sort([9, 1]) сортирует [9, 1], это назовем L1.
merge_sort([10, 2]) сортирует [10, 2], это назовем R1.

Для L1:

left=[9] и right=[1]
merge_sort([9]) возвращает [9] так как это базовый случай а merge_sort([1]) возвращает [1]
merge_sorted_lists([9], [1]) возвращает [1, 9]

То же самое происходит в R1 в там возвращается [2, 10]. В итоге merge_sorted_lists(L1, R1) возвращает результат.

Источник: https://miro.medium.com/max/1004/1*C1gVqHiClXu662JsMoRgUQ.png

Ханойские башни 🗼

Ханойские башни — это математическая задача, которая состоит из 3 колышков и, в данном случае, 3 дисков. Эта проблема в основном используется для обучения рекурсии, но она действительно используется в реальном мире.

Каждый диск имеет разный размер. Мы хотим переместить все диски в положение C так, чтобы самый большой находился снизу, второй по величине сверху самого большого, третий по величине (самый маленький) поверх всех них. В этой игре есть несколько правил:

Мы можем перемещать только 1 диск за раз.
Диск не может быть помещен поверх других дисков, которые меньше его.

Мы хотим использовать наименьшее количество возможных ходов. Если у нас есть 1 диск, нам нужно переместить его только один раз. Если у нас есть 2 диска, нам нужно переместить его 3 раза.

Количество ходов равно степени 2 минус 1. Если у нас есть 4 диска, мы рассчитываем минимальное количество ходов как 2⁴ = 16 — 1 = 15.

Чтобы решить приведенный выше пример, нам нужно сохранить самый маленький диск в буфере (1 ход). Ниже приведено решение Ханойской башни с 3 колышками и 3 дисками.

Обратите внимание, как мы используем буфер для хранения дисков.

Мы можем обобщить эту проблему. Если у нас есть n дисков: рекурсивно переместите n-1 из A в B, переместитесь с наибольшим из A в C, рекурсивно переместите n-1 из B в C.

Если есть четное количество фигур, первый ход всегда в середине. Если есть нечетное количество фигур, первый ход всегда на другой конце.

Рассмотрим кодирование алгоритма для ToH в псевдокоде.

function MoveTower(disk, source, dest, spare):
    if disk == 0, then:
        move disk from source to dest

Начнем с базового случая, disk == 0. source — это колышек, с которого начинаем. dest — конечный пункт назначения. spare запасной колышек.

FUNCTION MoveTower(disk, source, dest, spare):
IF disk == 0, THEN:
    move disk from source to dest
ELSE:
    MoveTower(disk - 1, source, spare, dest) // Step 1
    move disk from source to dest // Step 2
    MoveTower(disk - 1, spare, dest, source) // Step 3
END IF

Обратите внимание, что в шаге 1 мы переключаем dest и source. Мы не делаем это для шага 3.

С рекурсией мы можем быть уверены в 2 вещах:

У него всегда есть базовый случай (если этого не происходит, то как алгоритм узнает об окончании?)
Функция вызывает саму себя.

Алгоритм становится немного запутанным с шагами 1 и 3. Они оба вызывают одну и ту же функцию. Именно здесь начинается многопоточность. Вы можете запускать шаги 1 и 3 в разных потоках одновременно.

Поскольку 2 больше 1, мы снова перемещаем его еще на один уровень.

И так мы рассмотрели технику «разделяй и властвуй». Надеюсь вы поняли, как это работает и как выглядит код.

Далее, давайте узнаем, как формально определить алгоритм задачи, используя разделяй и властвуй. Эта часть является самой важной на мой взгляд. Как только вы это узнаете, будет гораздо проще использовать алгоритмы «разделяй и властвуй».

Числа Фибоначчи 🐰

Числа Фибоначчи очень известный ряд чисел. И его даже можно найти в природе. Например кролики размножаются в стиле чисел Фибоначчи. Так если у вас есть 2 кролика, они могут размножится до 3, 3 кролика размножаются до 5, 5 кроликов размножаются до 9 и так далее.

Числа начинаются с 1, и каждое последующее число равно текущее число + предыдущее число. 1 + 0 = 1. Затем 1 + 1 = 2. Потом 2 + 1 = 3 и так далее.

Мы можем описать это отношение с помощью рекурсии или повторения. Повторение — это уравнение, которое определяет функцию с точки зрения ее предыдущих входных данных. Повторение и рекурсия звучат одинаково и похожи.

С числами Фибоначчи, если n = 0 или 1, это приводит к 1. Иначе при любом другом n, рекурсивно добавляйте f (n-1) + f (n -2), пока не дойдете до базового случая.

Начнем с создания не рекурсивного калькулятора чисел Фибоначчи.

Мы знаем, что если n = 0 или 1, возвращаем 1.

def f(n):
    if n == 0 or n == 1:
        return 1

Числа Фибоначчи — это последние два числа, сложенные вместе.

def f(n):
    if n == 0 or n == 1:
      return 1
    else:
      fibo = 1
      fibroPrev = 1
      for i in range (2, n):
        temp = fibo
        fibo = fibo + fiboPrev
        fiboPrev = temp
      return fibo

Теперь когда мы поняли как это работает, давайте превратим это в рекурсию.

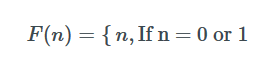
При создании повторения мы всегда начинаем с базового варианта. Базовый случай здесь, если n == 0 или 1, то вернуть n.

Если мы не вернем n, вместо 1, это приведет к ошибке. Например, F (0) приведет к 1. Когда действительно, это должно привести к 0.

Далее у нас есть формула. Если n не 0 или 1, что мы делаем? Мы вычисляем F (n — 1) + F (n — 2). В конце мы хотим объединить все числа вместе, чтобы получить наш окончательный результат. Мы делаем это, используя дополнение.

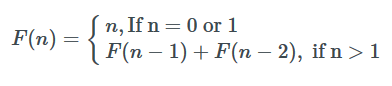
Это формальное определение чисел Фибоначчи. Обычно повторения используются, чтобы говорить о времени выполнения алгоритма «разделяй и властвуй».

def F(n):
  if n == 0 or n == 1:
    return n
  else:
    return F(n-1) + F(n-2)

Обладая знаниями «разделяй и властвуй», приведенный выше код становится чище и его легче читать.

Мы часто вычисляем результат повторения, используя дерево выполнения. Повелителям компьютеров 🤖 делать это не нужно, но людям полезно посмотреть, как работает ваш алгоритм «разделяй и властвуй». Для F(4) это выглядит так:

n равно 4, а n больше 0 или 1. Таким образом, мы делаем f (n-1) + f (n-2). Мы игнорируем дополнение на данный момент. Это приводит к 2 новым узлам, 3 и 2. 3 больше 0 или 1, поэтому мы делаем то же самое. То же самое для 2. Мы делаем это до тех пор, пока не получим группу узлов, которые равны либо 0, либо 1. Затем мы добавляем все узлы вместе. 1 + 1 + 0 + 0 + 1 = 3, что является правильным ответом.

Заключение 📕

Как только вы определили, как разбить проблему на множество мелких частей, вы можете использовать параллельное программирование для одновременного выполнения этих частей (в разных threads), тем самым ускоряя весь алгоритм.

Алгоритмы «разделяй и властвуй» являются одним из самых быстрых и, возможно, самых простых способов увеличить скорость алгоритма и невероятно полезны в повседневном программировании. Вот самые важные темы, которые мы рассмотрели в этой статье:

Что такое разделяй и властвуй?
Рекурсия
Сортировка слиянием
Ханойские башни
Кодирование алгоритма разделяй и властвуй
Числа Фибоначчи

Следующим шагом является изучение многопоточности. Выберите нужный язык программирования и наберите в поисковике фразу типа, «Многопоточность Python». Выясните, как это работает, и посмотрите, сможете ли вы решить любые проблемы в вашем собственном коде под этим новым углом зрения.

Вы также можете узнать о том, как использовать повторения (выяснение асимптотического времени выполнения повторения), о чем я и напишу в следующей статье. Если вы не хотите пропустить это или вам понравилась эта статья, рассмотрите возможность подписки на мой список рассылки 😁✨

Была ли вам полезна эта статья?

[14 / 4.3]